Publication

Second-order Democratic Aggregation, Tsung-Yu Lin, Subhransu Maji, Piotr Koniusz, European Conference on Computer Vision (ECCV), 2018 [paper + supplementary, bibtex, code ]

Summary

We study the relationship between democratic pooling and spectral normalization in the context of second-order features. Both these approaches generate an orderless aggregate of a set of features and were designed to equalize contributions in the aggregate improving performance than sum pooling. We present $\gamma$-democratic aggregators that interpolate between sum and democratic pooling outperforming both and achieving comparable results to the spectral normalization. Moreover the $\gamma$-democratic aggregations is computationally more efficient than spectral normalization and can be computed in a low dimensional space using sketching allowing the use of very high-dimensional second-order features which results in a state-of-the-art performance on several datasets.

Orderless feature aggregation

Given a sequences of features $\mathcal{X}=\{\mathbf{x}_1, \mathbf{x}_2, \cdots, \mathbf{x}_n\}$ encoded by $\phi(\mathbf{x})=\mathbf{x}\mathbf{x}^T$, the outer-product encoder, we are interested in functions for computing an orderless aggregation of the sequence to obtain a global descriptor $\xi(\mathcal{X})$. We study the following choices for computing $\xi(\mathcal{X})$ based on sum pooling: $$ \xi(\mathcal{X})=\sum_{\mathbf{x}\in\mathcal{X}}\phi(\mathbf{x}). $$ Second-order pooling were shown to be effective for semantic segmentation [Carreira et al.] and more recently for fine-grained recognition with deep CNNs (e.g., bilinear CNNs [Lin et al.])
  1. Democratic aggregation [Murray et al.] computes a weighted combination of features: $$ \xi(\mathcal{X})=\sum_{\mathbf{x}\in\mathcal{X}}\alpha(\mathbf{x})\phi(\mathbf{x}) $$ such that $\alpha(\mathbf{x})>0$ and satisfy: $$ \alpha(\mathbf{x})\phi(\mathbf{x})^T\xi(\mathcal{X})=C, \quad \forall \mathbf{x} \in \mathcal{X} $$ The above equation can be rewritten as: $$ \texttt{diag}(\mathbf{\alpha})\mathbf{K}\texttt{diag}(\mathbf{\alpha})\mathbf{1}_n=C\mathbf{1}_n $$ where $\mathbf{K}$ is the kernel matrix of the set $\mathcal{X}$ and $\mathbf{1}_n$ is a $n$-dimensional vector of ones. Although the solution to the above may not exist for arbitrary kernels, we show that with second-order features the solution always exists as long as none of the features are trivial, i.e., all zeros. Moreover the solution can be computed just as efficiently as the first-order counterpart using the kernel trick (see paper for details).
  2. $\gamma$-democratic aggregation. We propose a simple generalization of the above called $\gamma$-democratic aggregation where the weights $\alpha(\mathbf{x})$ satisfy: $$ \texttt{diag}(\mathbf{\alpha})\mathbf{K}\texttt{diag}(\mathbf{\alpha})\mathbf{1}_n=(\mathbf{K}\mathbf{1}_n)^\gamma $$ where the right-hand side of the equation takes the power of $\gamma$ in an elementwise manner. One can interpolate between sum pooling ($\gamma=1$) and democratic aggregation ($\gamma=0$) by adjusting the value of $\gamma$.
  3. Sum pooling + matrix power normalization [Lin and Maji, BMVC 17]. Let denote the matrix $\mathbf{A}$ obtained after sum pooling $\mathbf{A}=\sum\mathbf{x}\mathbf{x}^T=\mathbf{U}\mathbf{\Lambda}\mathbf{V}^T$. Matrix power normalization rescales the spectrum to obtain the final descriptor $\xi(\mathcal{X})$ $$ \xi(\mathcal{X})=\mathbf{A}^p=\Bigg(\sum_{\mathbf{x}\in\mathcal{X}}\mathbf{x}\mathbf{x}^T\Bigg)^p =\mathbf{U}\mathbf{\Lambda}^p\mathbf{V}^T, \quad p<\text{1} $$

Results

Equalizing feature contributions. While seemingly different, both democratic aggregation and power normalization aim at equalizing contributions among features. Formally lets define the contribution of a feature $\mathbf{x}$ as $C(\mathbf{x})$ given as $$ C(\mathbf{x}) = \phi(\mathbf{x})^T\xi(\mathcal{X}). $$ For democratic aggregation $C(\mathbf{x}) = 1/\alpha(\mathbf{x})$. In the paper we show that the variance of the contributions for the matrix normalization with a power $p$ satisfies $$ \sigma^2 < \frac{r^2_{\text{max}}\lambda_1^{2p}}{4\sum_{i}{\lambda_i^{2p}}}, $$ where $\{\lambda_i\}$ are eigenvalues in the descending order and $r_{\text{max}}$ is the maximum squared radius of the data $\mathbf{x} \in \mathcal{X}$. 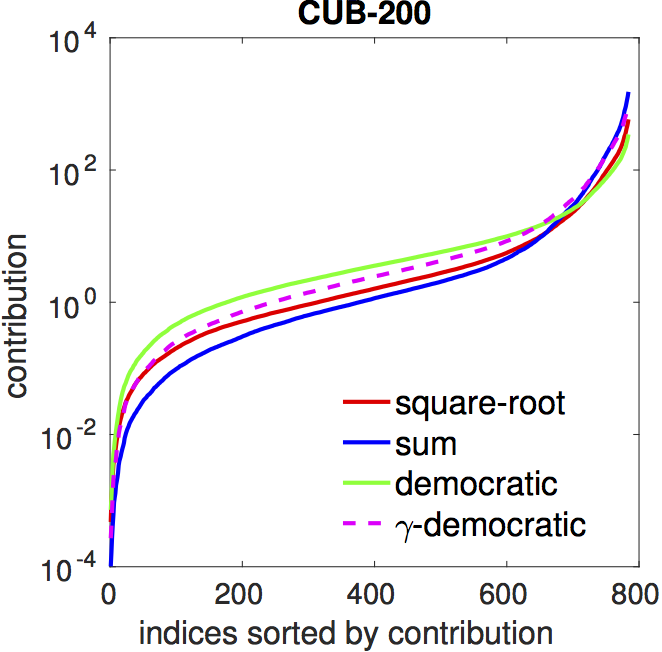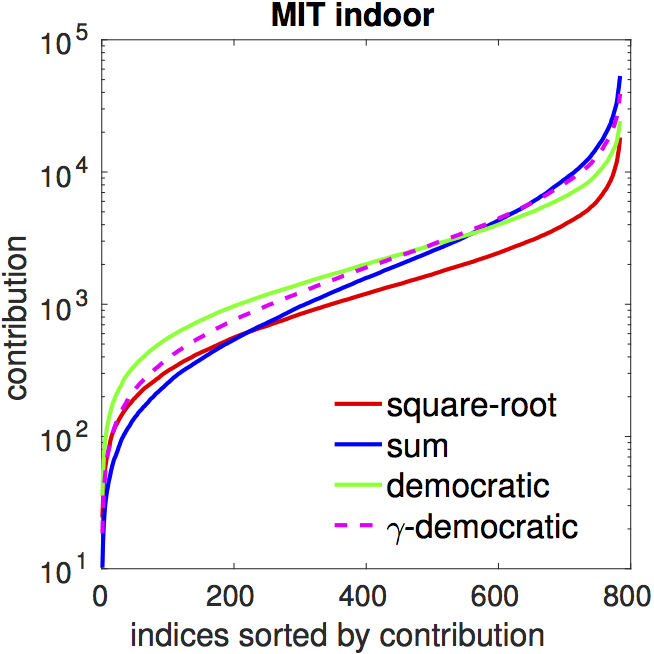The bound is minimized when $p=0$ which corresponds to whitening. The figure below shows the contributions for various pooling techniques. Both democratic aggregation (green) and matrix power normalization (red) equalize feature contributions resulting in flatter curves comparing to sum pooling (blue).
contributions

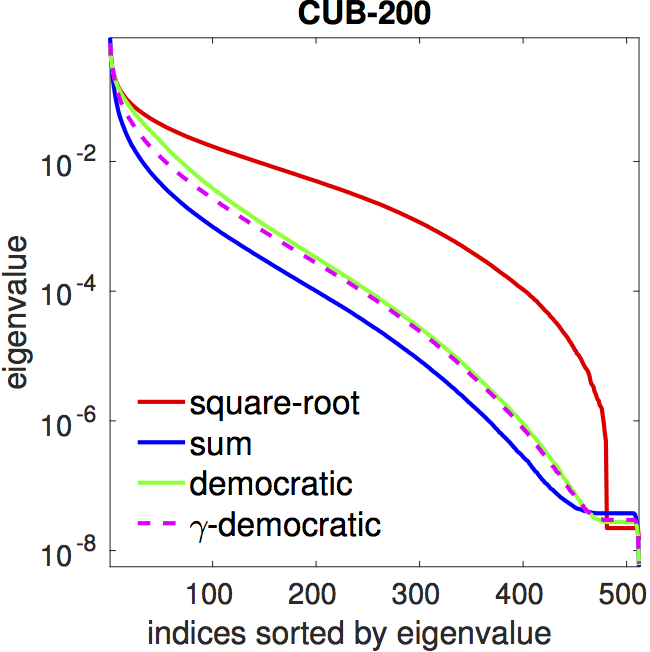
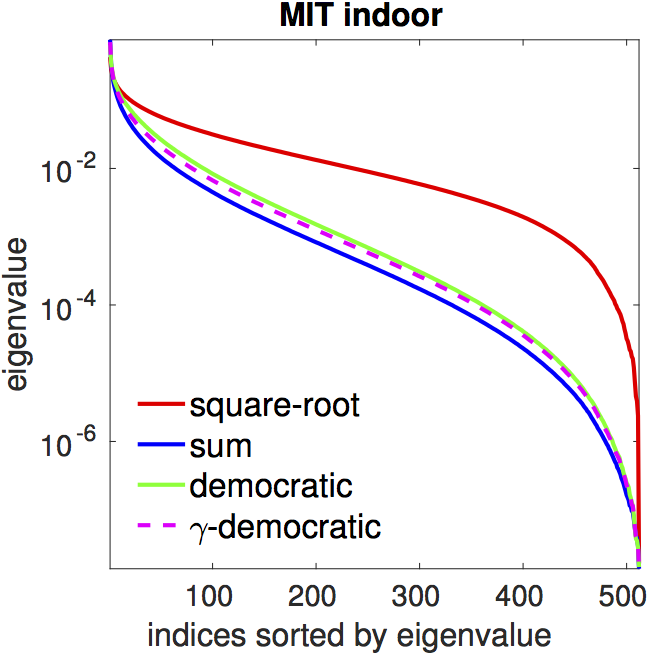
Flattening of the spectrum. Both democratic aggregation (green) and matrix power normalization (red) have a flatter spectrum compared to that of sum pooling (blue).
spectrum (eigenvalues)

Effect of $\gamma$ on accuracy with $\gamma$-democratic aggregation. The table below reports the accuracy using VGG-16 features on various fine-grained and texture recognition datasets. $\gamma$-democratic aggregation outperforms sum and democratic aggregation, while matrix power normalization performs best in most cases.

Dataset Sum    Democratic    $\gamma$-democratic    Matrix power normalization
Caltech UCSD Birds 84.0 84.7 84.9 85.9
Stanford Cars 90.6 89.7 90.8 91.7
FGVC Aircrafts 85.7 86.7 86.7 87.6
DTD† 71.2 72.2 72.3 72.9
FMD† 84.6 82.8 84.6 85.0
MIT Indoor 79.5 79.6 80.4 80.9
† Results on DTD and FMD reported using a single random split.

Accuracy using ResNet features with tensor sketching. Despite offering higher accuracy matrix power normalization is computationally expensive and memory intensive, even with iterative approximate methods. In contrast, democratic pooling is computationally efficient and can be combined with tensor sketching allowing the use of higher dimensional features such as the 2048-dimensional ResNet features. Naive second-order pooling with matrix normalization would require 2048x2048 dimensional representations. The resulting baseline beats or matches the state of the art on various datasets.
Method    MIT Indoor
Places-205 80.9
Deep Filter Banks 81.0
Spectral Features 84.3
FASON 81.7
$\gamma$-democratic (ours) 84.3
Method      FMD      DTD
IFV+DeCAF    65.5 ∓ 1.3    69.4 ∓ 1.2
FV+FC+CNN    82.2 ∓ 1.4    75.5 ∓ 0.8
LFV    82.1 ∓ 1.9    73.8 ∓ 1.0
SMO Task    82.3 ∓ 1.7    -
FASON    82.1 ∓ 1.9    72.9 ∓ 0.7
$\gamma$-democratic (ours)    84.3 ∓ 1.5    76.2 ∓ 0.7

Acknowledgements

We acknowledge support from NSF (#1617917, #1749833) and the MassTech Collaborative grant for funding the UMass GPU cluster.

References